Group Project

Our group: Igor and Alex, have our group blog on the following link (including the program and photos taken throughout the project)

http://physics4chunteririanto.blogspot.com/

Da Last Lab!!!

Planck's Constant from LED

Purpose: to estimate and calculate the value of Planck's constant using everyday light source.


Procedure:
This lab explored one of the nature of light's energy: E = h f = hc/λ
By knowing (or estimating) λ, and since c is a constant, Planck'cs constant can be calculated since it is proportional to Energy. Two different diodes: blue and yellow were used. Each wavelength λ was estimated roughly to be 450 nm for blue and 590 nm for yellow.
When one looked through diffraction grating, one see a blue line on the blue diode and yellow for yellow, as expected. This confirms that the diodes were mostly monotone/ coherent (only reflects a narrow range of color; instead of seeing many lines, only blue line is observed).

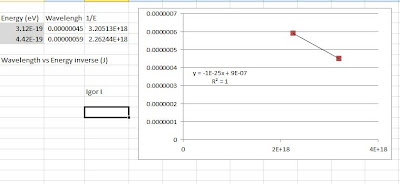
Calculation and data:

First, energy was estimated from the Voltage. It was found that E_blue = 1.95 eV and E_yellow = 2.76 eV.
Since E = hc/λ and c is constant; E = 1/λ or 1/E = λ.

The graph of 1/E vs λ

The slope is the planck's constant.

Slope, m is roughly 1.50e-25 and is equal to hc. Dividing with c, the value of 5.00e-34. (actual h = 6.62e-34; % difference = 24.5%)

Error:

The large percent error (24.5%) is due to the approximation of the wavelength of the diodes (estimated to be 450 nm and 590 nm from online source). 

Another room for error is due to the electric potential. Although potential was more accurate than wavelength, the potential was not truly exact due to many other uncounted external resistors.

Light and Matter Waves

Purpose:
Using python (spyder) to create a visual representation of light's diffraction.

An example of the code is as follows:
from visual import *
import pylab as p
import mpl_toolkits.mplot3d.axes3d as p3
wavelength = 8.0e-3
scrnDist = 5.0e-2
scrnWdth = 2.4e-2
xs = 0
ys = 0
A = 1
N = 100
dX = scrnDist / N
Xcoords = arange(dX,scrnDist + 2* dX, dX)
dY = scrnDist / N
Ycoords = arange(-scrnDist / 2, scrnDist/2+2 * dY, dY)
[xd, yd] = meshgrid(Xcoords,Ycoords)
r = sqrt((xd - xs)**2 + (yd - ys)**2)
E0 = A * cos(2*pi*r/ wavelength)/r
print Xcoords
print Ycoords
print r
print E0
fig=p.figure()
Efield = p3.Axes3D(fig)
Efield.plot_wireframe(xd,yd,E0)
Efield.set_xlabel('Xd')
Efield.set_ylabel('Yd')
Efield.set_zlabel('E0')
fig2 = p.figure()
p.contour (xd,yd,E0)
p.show()

1.1
Graph visualizing the varying Efield on x,y, and z coordinates. z axis represents the quantity of E0 (E_field)

Wavelength = 4 mm

1.2

Graph of Efield when wavelength is 8mm

This shows that magnitude of E field varies in respect to wavelength. The "ripples" also varies; the higher the wavelength, the smoother the ripples (high wavelength shows no ripples / fat surface)

Contour plot of  fig 1.2

The next part measures and visualizes fields of two point-sources (where interference starts to occur)

The 2 holes-interference is shown as (wavelength = 50 mm to show the "flattening" of the surface):

2.0

Wavelength = 50 mm. Notice the red dot on contour graph, showing the high intensity caused by high wavelength value.

2.1 

Wavelength = 4.0 mm.

Next part will focus on measuring the intensity.

Th wavelength will be modified to 600 nm, screen width 30 mm and distance 50 mm, wand source separation 0.016 mm.

3.0

The 2-D graph of intensity

Spectra Lab

Purpose: 
To observe the various color spectra through small slits: to view what a white light is composed of , and to measure the spectra of hydrogen gas. The spectra will be observed by calculating its wavelength obtained by measuring the distance/ separation of each spectra.

Materials: 
White light source
Meter sticks
Diffraction lens
Marker
Various gas (light source)

λ/d = D/(L^2 + D^2)^0.5

or

λ = D * d / (L^2 + D^2)^0.5

λ is the wavelength of each spectrum

D is the distance from light source to observer

d is the distance between the slits

(L^2 + D^2)^0.5 is the distance from observer to the spectrum (forms a triangle)

I. Measuring spectra of white light

White light consists of all colors, as shown above^. The first part of the experiment measures the location of each color to determine the wavelength of each color.

Length is 1.00 m + 0.05 

d is 2*10^-6 m

The colors, in order, are as follows:

	Violet	Indigo	Blue	Green	Yellow	Red
D (m)	0.199	0.223	0.251	0.289	0.303	0.411
λ	3.90346E-07	4.35308E-07	4.86897E-07	5.5528E-07	5.7996E-07	7.6029E-07
λ actual	0.0000004	0.000000445	0.000000475	0.00000051	0.00000059	0.00000065

Calibration graph (y axis = actual value, x axis = observed values)

λ adjusted

3.6766E-07

3.9849E-07

4.33865E-07

4.80753E-07

4.9768E-07

6.21331E-07

The adjusted λ ranges from 370 to 620 nm; this is because the graph itself is not linear. R squared is 0.93, which is far from 1. It is expected to see adjusted λ values that is off from the actual values.

wavelength in nm

390.345995

435.3076116

486.8967555

555.276344

579.9616666

760.2899278

Uncertainty in nm

4.82700251

4.846194215

5.948377766

22.638172

5.019166705

55.14496391

Wavelength with uncertainties: 

λ1 = 390 + 4.8 nm

λ2 = 435 + 4.8 nm

λ3 = 487 + 5.9 nm

λ4 = 555 + 23 nm

λ5 = 580 + 5.0 nm

λ6 = 760 + 55 nm

II. Measuring spectra of unknown gas and hydrogen

The second part of the experiment, an unknown gas and a hydrogen light sources were used. Different light spectra were observed.

(The unknown that was assigned was unknown #3, which was He)

D and wavelength are as follows:

He spectrum observed values:

	Violet	Blue	Green	Yellow	Red
D (m)	0.216	0.242	0.276	0.324	0.373
λ (nm)	394.1	442.7	505.1	572.9	674.1

Actual values:

Actual
λ (nm)	438.8	447.1	501.6	587.6	667.8

Calibration: y = 0.877x + 74.6 

Uncertainty

22.35

2.2

1.75

7.35

3.15

λ1 = 394.1 + 22.35 nm

λ2 = 442.7 + 2.2 nm

λ3 = 505.1 + 1.75 nm

λ4 = 674.1 + 3.15 nm

Hydrogen Spectrum

Observed values:

	Violet	Green	Yellow	Red
D (m)	0.221	0.252	0.282	0.308
λ (m)	4.31586E-07	4.89E-07	5.43E-07	5.89E-07
λ (nm)	432	489	543	589

Actual
λ (nm)	435	520	565	625

Calibration: y = 1.17x - 65.7 

Uncertainty

1.5

15.5

11

18

λ1 = 432 + 1.5 nm

λ2 = 489 + 15.5 nm

λ3 =543 + 11 nm

λ4 = 625 + 18 nm

Conclusion:

The spectra lab measures the different emitted light spectra when light travels through the diffraction gratings (small slits), causing the object (light source) to emit emissions of different wavelengths. The first experiment measures normal white light source. It appears that white light source emits all the visible color. The second and third experiment measures hydrogen and unknown (helium) gas light source. Being different from white light source, the spectra appears to be single lines. The wavelength of each corresponding lines could be measured by finding the distance (D) from the light source. Most of the measurements have uncertainty ranging from 5-20 nm, with few spectra exhibiting uncertainty of >20 nm, and one >50 nm.

Active Physics Lab - Laser

Purpose:
To analyze what's going on inside a laser.

Materials:
Decent computer with java installed
http://wps.aw.com/aw_young_physics_11/13/3510/898597.cw/index.html

Question 1: Absorption
At any given time, the number of photons inputted into the cavity must be equal to the number that have passed through the cavity without exciting an atom plus the number still in the cavity plus the number of excited atoms. Verify this conservation law by stopping the simulation and counting photons.

At any given time, N_in = N_out + n_2 (# atoms in excited state) + #photons in cavity.
In this case, N_out (2) + n_2 (6) + 0 = N_in = 8.


Question 2: Direction of Spontaneous Emission
During spontaneous emission, does there appear to be a preferred direction in which the photons are emitted?

No, the direction of emitted photons appeared to be completely random and having no preferred direction.


Question 3: Lifetime of Excited State
Does there appear to be a constant amount of time in which an atom remains in its excited state?

No. The time an atom stays in excited state is random, because the traveling photons appear to be traveling randomly; whichever atom happens to be in the way of the photon will transition. 

Question 4: Stimulated Emission
Carefully describe what happens when a photon interacts with an excited atom. Pay careful attention to the phase and direction of the subsequent photons. (Can you see why this is called stimulated emission?)

When a photon interacts with an excited atom, the excited atom will transition and emits a photon, emitting a net photon of 2 (incident photon + emitted photon). When those photon group hits another excited atom, that atom will also emits one more photon, emitting 3 net photons. 
Every time a photon(group) interacts with an atom, it will come out having one more photon.


Question 5: Pumping
Approximately what pumping level is required to achieve a population inversion? Remember, a population inversion is when the number of atoms in the excited state is at least as great as the number of atoms in the ground state.

A pumping level of at least 75 is required to have an average of at least as many excited atoms as ground state. 

Question 6: Photon Emission
Although most photons are emitted toward the right in the simulation, occasionally one is emitted in another direction. Are the photons emitted at odd directions the result of stimulated or spontaneous emission?

Spontaneous emission. It cannot be stimulated by stimulated emission because stimulated emission's photons must go the same direction as the incident photons, which is to the right. 

Since spontaneous emission occurs naturally, without external interference, photons emitted from spontaneous emission could go to any direction. 

Consequently however, a spontaneous- stimulated emission could also cause the emitted photon to travel to any directions, although the probability of this happening is relatively small.

Active Physics lab - Relativity

Purpose:
To further analyze Einstein's 2nd postulate, which leads to relativity; which states that no object travels faster than speed of light.

Material:
A working laptop with internet connection and java.
Website: http://wps.aw.com/aw_young_physics_11/13/3510/898597.cw/index.html
'
Questions were to be answered from section 17.1 and 17.2


17.1
Question 1: Distance traveled by the light pulse
How does the distance traveled by the light pulse on the moving light clock compare to the distance traveled by the light pulse on the stationary light clock?

Distance traveled by light on moving clock is "slower" than stationary clock.
In fact, it is off by γ factor, which was set to be 1.45. (Light on moving travels 1.45 times slower to an outside observer)


Question 2: Time interval required for light pulse travel, as measured on the earth
Given that the speed of the light pulse is independent of the speed of the light clock, how does the time interval for the light pulse to travel to the top mirror and back on the moving light clock compare to on the stationary light clock?

γ was set to be 1.41. The time on stationary was 6.67 and moving 9.40. 9.40s and 6.67s were related by a factor of 1.41, which was the value of constant.

 Question 3: Time interval required for light pulse travel, as measured on the light clock
Imagine yourself riding on the light clock. In your frame of reference, does the light pulse travel a larger distance when the clock is moving, and hence require a larger time interval to complete a single round trip?

No, the time in moving time reference does not differ from the time of rest frame. Although according to stationary observer, light travels slower.

Question 4: The effect of velocity on time dilation
Will the difference in light pulse travel time between the earth's timers and the light clock's timers increase, decrease, or stay the same as the velocity of the light clock is decreased?

The difference in light travel time is slower (decreased) as velocity is decreased. (As v -> 0, γ -> 1).

Question 5: The time dilation formula
Using the time dilation formula, predict how long it will take for the light pulse to travel back and forth between mirrors, as measured by an earth-bound observer, when the light clock has a Lorentz factor (γ) of 1.2.

Δt = γΔt_proper

1.2 = γ

1.2 = 1/(1-v^2/c^2)^0.5

solving for v yields

v = c/1.2 * (1.2^2 - 1)^0.5

v = 165,831,239.52 m/s

Question 6: The time dilation formula, one more time
If the time interval between departure and return of the light pulse is measured to be 7.45 µs by an earth-bound observer, what is the Lorentz factor of the light clock as it moves relative to the earth?

Solving for γ, 

γ = Δt / (Δt + 7.45μs)

17.2

Question 1: Round-trip time interval, as measured on the light clock
Imagine riding on the left end of the light clock. A pulse of light departs the left end, travels to the right end, reflects, and returns to the left end of the light clock. Does your measurement of this round-trip time interval depend on whether the light clock is moving or stationary relative to the earth?

Yes. The length "contracts" as the object travels relatively "fast." The faster the object moves (the closer its constant velocity to the speed of light, the shorter the distance / length is).

Question 2: Round-trip time interval, as measured on the earth
Will the round-trip time interval for the light pulse as measured on the earth be longer, shorter, or the same as the time interval measured on the light clock?

Depends on whose frame of reference is measuring it. In the frame of the traveling clock, the time will be the same as the stationary one measured by a stationary observer. If the time of traveling clock is measured by a stationary observer, then: 1. length/ distance will appear shorter/ less, and 2, time it takes for the light to travel will be longer.

Question 3: Why does the moving light clock shrink?
You have probably noticed that the length of the moving light clock is smaller than the length of the stationary light clock. Could the round-trip time interval as measured on the earth be equal to the product of the Lorentz factor and the proper time interval if the moving light clock were the same size as the stationary light clock?

γ was set to be 1.41. Time was 6.61, while time proper was 9.50. They were off by γ factor, or 1.41 (refer back to time dilation). Since distance/ length is velocity * time, since time is longer in a moving object and it must always equal to velocity v (constant), then distance must decrease proportionally (by factor of γ).

Yes, the time interval as measured by earth (rest frame) is equal to lorentz factor γ times proper time interval (moving), hence Δt = γ(Δt_p)

Question 4: The length contraction formula
A light clock is 1000 m long when measured at rest. How long would earth-bound observer's measure the clock to be if it had a Lorentz factor of 1.3 relative to the earth?

L_p = 1000m

γ = 1.3

L = (L_p)/γ

L = 769.23 m

Experiment 12

Exp 12
Diffraction

Purpose: To use diffraction of light to determine the length of CD grooves (width [a] of the openings) by measuring the length between the reflected rays using diffraction grating equations.

Materials: 
Diode laser
CD
Reflecting surface (white board)
Meter stick(s)
Stands (wooden blocks)
Diffraction film

Procedure:
Since λ of diode laser was not known, it has to be calculated first.
To calculate the wavelength of the laser, a diffraction film of known d (distance between slits) was used. In this case, it was 500 slits / mm. Reciprocating it,
d = 2*10^-3 mm.
The formula used was

d sin(θ) = m λ,

solving for λ,

λ = d sin (θ)/ m

The angle could be found experimentally. First, the laser was aimed perpendicular to the diffraction film; the ray would diffract and at least three rays would be shown on the reflecting surface. The angle was the arctangent of the distance between the diffraction film to the reflecting surface over the distance between the first light (1st maxima) to third light (3rd maxima).
Using formula above, θ was 40.32 degree. λ then, is  647.6 nm.

With λ known, the grooves can be calculated. The formula used is

a sin (θ) = m λ

a = m λ/ sin (θ

The CD was positioned so that when laser was aimed towards it, its ray would reflect to the surface orthogonal to it. The distance (d) from the CD to the surface was 68.5 + 0.1 cm The distance between the two lights observed was 28.8 + 0.1 cm. Using phytagorean principles, the angle was calculated to be 22.8 degrees.

Using the equation previously mentioned and letting m = 1 (first maxima), a was calculated to be 1671 nm.

Uncertainty and Error Analysis:

*The slits was assumed to be a constant number without error (it was not measured in the lab). 

ud = 0

*The angle, however, had uncertainty. The triangle was found using two length measurements. 

tan (θ) = (Length / Width);

θ = arctan (Length / Width);

uθ = ((L ln (W) 1/(1+L/W) uW)^2 + (1/W* (1/(1+L/W)) uL)^2)^(0.5)

uθ = 0.45 degree

λ(d, θ) = d sin (θ)/ m

dλ/dd = sin (θ) / m 

dλ/dθ = d cos(θ) / m

uλ = ((sin (θ) / m  * ud)^2 + (d cos(θ) / m * uθ)^2)^(0.5)

uλ = 3.43*10^-7 m = 343 nm

λ then, is 647.6 nm + 343 nm

The second calculation has angle with different uncertainty. Using the same formula:

uθ = ((L ln (W) 1/(1+L/W) uW)^2 + (1/W* (1/(1+L/W)) uL)^2)^(0.5)

uθ = 8.57 degrees

a(θ,λ)  =  λ / sin (θ)

da/ dλ = 1 / sin(θ)

da/ dθ = - λ cot(θ)/ sin(θ)

ua = ((1/ sin(θ) * uλ)^2 + (- λ cot(θ)/ sin(θ) * uθ)^2)^(0.5)

ua = 34070 nm

a = 1671 + 34070 nm

Normal CD grooves usually range between around 1500 nm. The calculated values, including the uncertainties, definitely falls within the range. 

Errors (comment on the large uncertainty value):

The large uncertainty value could be caused by several reasons, one of them being having to do the experiment twice. The wavelength of the laser was unknown initially and had to be determined by performing  an additional experiment. When performing this, some errors were recorded and accumulated throughout the lab. Those error later further were being accumulated and added up along with the second experiment's uncertainties, causing the values to substantially increased to what was calculated above. 

Further error analysis:

Although the calculated value of 1671 nm falls within about 10% of the expected value of 1500 nm, it was not exact due to several factors. One of them was the experimented CD had been used previously; it was a burned CD; a burned CD probably had a different slit density than a new CD. Secondly, the CD was from at least 2002, 10 years prior. CD-ROM technology had change the past decade. CDs today had an improved memory capacity than a decade ago; an increase in memory capacity implied that it had different slit density. 

Another room for error was when experiment was performed, it was not truly observed whether the ray was perfectly orthogonal to the surface or not. If it was not, then the calculated angle of 22.8 degrees would not be perfectly accurate, hence the calculated a value would be different. 

The inconsistency of the distance could not be found using the obtained data, because it would require two reflections on two different locations on the CD, which was not performed in this experiment, unfortunately.

Experiment 6

Exp 6
Speed of Sound

Purpose: To use fundamental frequency and spinning slinky to determine the speed of sound

Material:
Long, hollow, red plastic tube with one end closed
LoggerPro software
Measuring stick

Procedure:
Have the plastic tube spinning forming a circle. Use loggerpro software to measure the angular velocity, ω. Do the experiment several times to find several calculated values for velocity. 

v =λ f

(A.)

Frequency may be obtained by recalling that

ω = 2πf, giving 

f = ω/2π 

(B.)

While wavelength, λ, can be found by assuming that the wave pattern inside the tube would be harmonic wave:

(2n+1) λ/2 = L

 (C.)

whereas n is the number of harmonics and L length of pipe.

After λ and f were found, v, the speed of sound, can be calculated and compared.

Data and Uncertainty:

Length of pipe is 0.83 +/- 0.05 m

Two trials were conducted.

Trial 1:

ω = 3859 +/- 1 rad/s

f = 614 +/- 1 s^-1

Trial 2: 

ω = 5068 +/- 1 rad/s

f = 807 +/- 1 s^-1

The harmonics were found using the speed of sound, 340 m/s.

v = λf

v/f = λ

whereas from equation (C.), λ = 2L / (2n+1).

Both n's for trial 1 and 2 are 2+/- 0 and 3+/- 0, respectively (the uncertainty was 0 because if it were to be, for example, 2 +/- 0.05 carried from length, there is no such thing as 0.05 harmonics. Harmonics' value must be in integers).

n_1 = 2

n_2 = 3

From n, λ can be solved backwards,  using 

λ = 2L / (2n+1)

Trial 1:  λ = 0.56 +/- 0.05 m

Trial 2:  λ = 0.43 +/- 0.05 m

Putting the data together:

Trial 1: f = 614 +/- 1 s^-1, λ = 0.56 +/- 0.05 m

Velocity then, using equation (A.), is 343.84 +/- 1.05 m/s

Trial 2: f = 807 +/- 1 s^-1, λ = 0.43 +/- 0.05 m

v = 347.01 +/- 1.05 m/s

Whereas speed of sound at the sea level, according to https://www.google.com/, is 340.29 m/s

Although it does not fall within uncertainty values, the values were off by within less than 2.00% error, which can be considered insignificant. It was very close to the actual speed of sound.

Error Analysis:

Some of the possible rooms for error were the measurement of the length. The pipe had to be assumed initially to have constant diameter and did not deform when swung. Being a plastic pipe, some deformity must have occurred. This would alter the sound travel a little.

Second room for error was the rounding of harmonics, n. One value obtained was less than 3 (around 2.84, but it was rounded up to three). This altered the value by almost 10%.

END OF LAB 6.

Physics 4C complimentary guitar solo live performance